By Andy | February 7, 2005 | 0 Comment

I came across an interesting problem today.
Consider a Circle, inside the circle inscribe a triangle, inside that triangle inscribe a circle, then inside that circle inscribe a square, then another circle, then a pentagon and so on…
The question is does this sequence of shapes converge to a point, or a circle? And if it converges to a circle what is it’s radius?
Now we can start to build up our solution as outlined below:
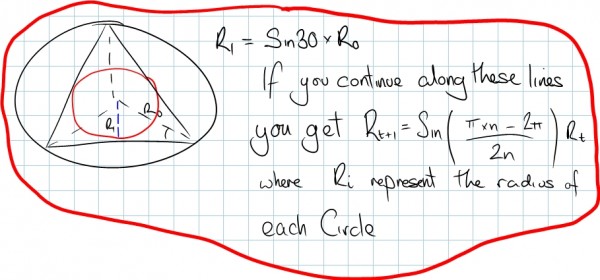
So we have now got a recursive definition for the radius of the circle, in the form:
\(R_{n+1} = sin(\frac{n \pi- 2 \pi}{2n})R_{n}\)If we now apply the subtraction formula for Sine:
\(sin(a-b) = sin(a)cos(b)-sin(b)cos(a)\)Then we obtain:
\(sin (\frac{n \pi- 2\pi}{2n}) = sin(\frac{\pi}{2}- \frac{\pi}{n}) = sin(\frac{\pi}{2})cos(\frac{\pi}{n})- sin(\frac{\pi}{n})cos(\frac{\pi}{2})\)But \(sin(\frac{\pi}{2}) = 1 and cos(\frac{\pi}{2}) = 0\)
so the above simplifies to
\(sin(\frac{\pi}{2}- \frac{\pi}{n}) = cos(\frac{\pi}{n})\)So our recursive formula is now:
\(R_{n+1} = cos(\frac{\pi}{n})R_{n}\)So we now have a formula for the radius of each circle based up the radius of the last one.
So the radius of the nth Circle (i.e. the circle inscibed in the polygon of side n) can be expressed as:
\(R_{n} = \LARGE \displaystyle\prod_{t=3}^{n} \Large cos(\frac{\pi}{t}) R_0\) where \(R_0\) represents the initial radius.
We start at \(n=3\) becuase this represent the first polygon – the triangle.
The next question though is does this tend to a limit?
Using Excel I checked the first 5000 terms of \(\LARGE \displaystyle\prod_{t=3}^{\infty} cos(\frac{\pi}{t})\) and it seems to tend to 0.115038839…
Next I need to prove that the function actually tends to a non-zero limit! But that will have to wait till I have worked out how to prove it!!
The trick is to convert the infinite product into an infinite sum… To do this we need to find a why to turn multiplication into addition. What do we know that does this? The LOG function!!
So: \(log \Bigg[ \LARGE\prod_{n=3}^{\infty} \Large cos(\frac{\pi}{n}) \Bigg] = \LARGE \sum_{n=3}^{\infty} \Large log \Big[ cos(\frac{\pi}{n}) \Big]\)
So now that we have an infinite sum, what do we need to do to show that it converges to a limit?
After much struggling and racking of my brain, I suddenly remembered the Integral Test.
This tells us that if our function is:
* Continuous
* Positive
* Decreasing
Then if the integral of the function:
is convergent then,
\(\LARGE \sum_{1}^{\infty}\Large a_i\)where \(a_i=f(i)\) is also convergent.
So what do we need to do?
Well our function \(f(x) = log(cos(\frac{\pi}{n}))\) is continuous but it is negative and increasing…
So let our new function \(g(x) =-f(x) =-log(cos(\frac{\pi}{n}))\)
So \(g(x)\) is now continuous, positive and decreasing. Which means we can now apply the Integral Test!
Now we could fudge our function sothat we evaluated it between \(1\) and \(\infty\), but this wouldn’t effect the result. So instead we will evaluate it between \(3\) and \(\infty\).
Using my new best friend Mathematica (downloaded a 15 day trial from their website) I was able to evaluate the definite integral
\(\displaystyle\int_3^\infty -log(cos(\frac{\pi}{n})) dx \approx 1.76859\) which is convergent!
Which by the *Integral Test* tells us our sum
\(\LARGE \sum_{n=3}^{\infty} \Large log \Big[ cos(\frac{\pi}{n}) \Big]\) is convergent to a non-zero value (all values are non-zero, so the summost be non-zero)
Hence our initial product:
\(\LARGE\prod_{n=3}^{\infty} \Large cos(\frac{\pi}{n})\)Must also be convergent to a non-zero value.
So we have now proved that if we start with a Circle and inscribe a triangle, then a circle, then a sqaure,…
Then this does not tend to a point. Instead it tends to a circle with a radius that is non-zero.
To evaluate this radius numerically we need to use a computer as it not possible (as far as I am aware) to express the constant in terms of any other nice constants such as \(\pi, e\)…
Using *Mathematica* again it was possible to evaluate it more accuratley as:
0.1149420448532962
So the limit of the product which is approximated by the above number represents the ratio of the radius of the outermost circle to the radius of the circle which marks out the limit of this geometric sequence…
If you spot any mistakes or have anything to add stick it in the comments!